Man kan let overbevise sig om, at en plan polygon har lige mange hjørner og kanter, og Euler opdagede, at man har en tilsvarende formel for polyedere:
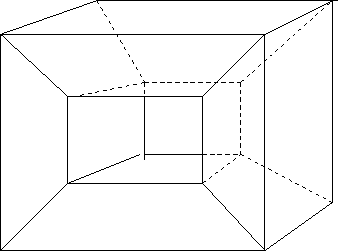
Hvis man ikke fortæller præcist, hvad man mener med et polyeder, og f.eks. tillader figuren nedenfor, er resultatet ikke 2 (i dette tilfælde er det 0). Problemet er, at denne figur ikke ``ligner'' ( er homeomorf med ) en kugleflade, og Eulers formel ovenfor gælder kun for polyedere, der er homeomorfe med en kugleflade.
Denne opdagelse er brugt som et eksempel på matematikkens udvikling og videnskabsteori i Imre Lakatos' bog Proofs and Refutations. The logic of mathematical discovery. Cambridge University Press 1976. Umiddelbart skulle man jo tro, at det er en svaghed ved polyederformlen, at den kun gælder for polyedere, der ``ligner`` kuglefladen.
Jeg gør i foredraget rede for, at denne ``defekt'' ikke er en svaghed, men tværtimod en styrke ved polyederformlen. Det er nemlig det, der gør, at polyederformlen giver, hvad vi i algebraisk topologi kalder en topologisk invariant. Jeg vil fortælle lidt om, hvad sådan nogen kan bruges til, og desuden vil jeg bevise formlen.
