Opgave 2
Vi kan eventuelt skrive F på følgende måde:
![]()
| (1) |
(a) Fra Slides, side 15 ved vi at den lineære approximation omkring ![]() har formen:
har formen:
![]()
Det betyder at tangentplanen til grafen i punktet ![]() har ligning
har ligning ![]()
I vores tilfælde skal vi blot indsættet ![]() i stedet for
i stedet for ![]() .
.
Vi differentierer: ![]() og
og ![]() og indsætter punktet
og indsætter punktet ![]() :
: ![]() og
og ![]() Desuden er
Desuden er ![]()
Vi får ![]()
Tegning af grafen og tangentplanen:
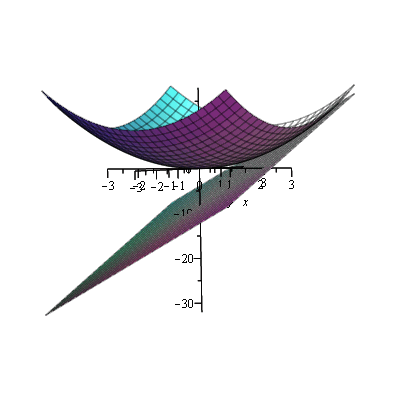 |
(b) Vælg f.eks. ![]() . Så er
. Så er ![]()
| (2) |
Den lineære approximation: ![]()
| (3) |
Den lineære approximation er tættere på ![]() hvis
hvis ![]() er tættere på
er tættere på ![]()
Opgave 3
(a) Lad ![]() angive afstanden mellem det ukendte punkt
angive afstanden mellem det ukendte punkt ![]() og punktet
og punktet ![]()
Tilsvarende er ![]() ,
, ![]() og
og ![]()
Vores observationer så (ikke-lineariseret) ![]()
For at finde den lineariserede observationsligning skal vi bruge formlen side 22 i Slides.Rækkerne i ![]() er gradientvektorer for funktionerne hhv.
er gradientvektorer for funktionerne hhv. ![]()
hvor punktet ![]() indsættes.
indsættes.
På højresiden indsættes ![]() og
og ![]() hvor
hvor ![]() Altså
Altså
](images/svar3_38.gif)
Gradientvektorer er udregnet for denne type af funktioner på side 25 i Slides.
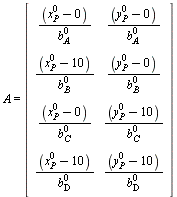
Den lineariserede observationsligning er så (Slides, side 22):
)) = `+`(b, r)](images/svar3_40.gif)
hvor 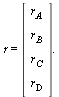 Vi kan eventuelt skrive
Vi kan eventuelt skrive ![]() og
og ![]() i stedet for
i stedet for ![]() og
og ![]() .
.
(b) Nu indsættes ![]() Så er
Så er ![]() . Tilsvarende er
. Tilsvarende er ![]()
Dermed er ](images/svar3_49.gif) og
og 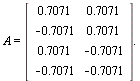
Normalligningen , true) = Typesetting:-delayDotProduct(`^`(A, T), b, true)](images/svar3_51.gif) bliver så
bliver så
![]()
Altså ![]() og derfor
og derfor ![]() . Vi sætter derfor
. Vi sætter derfor ![]()
(c) Så er ![]() Desuden er
Desuden er ![]()
Nu er 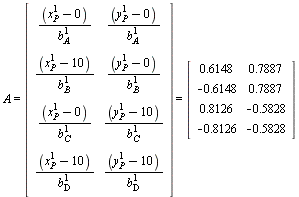 og
og 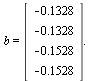
Normalligningen ![]() har løsning
har løsning ![]()
Vi finder altså ![]() .
.
(d) På samme måde finder vi ![]() Altså
Altså ![]() .
.
(e) Fixpunkterne og afstandene til det ukendte punkt er symmetrisk omkring aksen med ligning ![]() . Da vi starter på denne linie med
. Da vi starter på denne linie med ![]() vil vi blive på denne linie.
vil vi blive på denne linie.
(f) Afstand til A og B: ![]() . Afstand til C og D:
. Afstand til C og D: ![]() .
.