linearalgebraex1.mw
Solving Linear Algebra problems using Maple.
Start by loading the linear algebra package
Vectors and matrices are defined as follows.
| > |
A:=Matrix([[1,2,1],[2,4,-2]]); |
Matrix-vector product
Finding the echelon form (not unique)
| > |
GaussianElimination(A); |
Finding the reduced row echelon form (unique)
| > |
ReducedRowEchelonForm(A); |
Warning, does not work for matrices with parameters. Two examples:
| > |
B:=Matrix([[1,2,1],[2,4,h]]); |
| > |
ReducedRowEchelonForm(B); |
This is wrong for h=2.
| > |
C:=Matrix([[u,v],[w,z]]); |
| > |
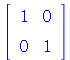
ReducedRowEchelonForm(C); |
This is wrong for many different values of the four parameters in this matrix.
Solving a system of linear equations
Define the coefficient matrix and the right hand side, as in the following examples. Then use the linear solver.
| > |
F:=Matrix([[1,2,3],[3,1,2],[-1,-1,-1]]); |
If the solution is not unique, then Maple returns the solution in parametrized form.
| > |
G:=Matrix([[1,2,3],[2,1,4]]); d:=Vector([2,2]); |
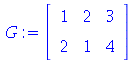
Maple uses a particular notation for variables it defines. They always start with an underscore _
You can make Maple use any name you choose, giving it as a string in the input. The above example again, with this option.
| > |
LinearSolve(G,d,free='t'); |
](images/linearalgebraex1_31.gif)
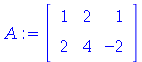
](images/linearalgebraex1_33.gif)
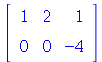
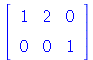
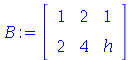
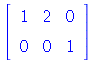
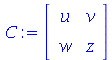
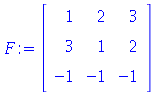
](images/linearalgebraex1_41.gif)
](images/linearalgebraex1_42.gif)
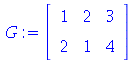
](images/linearalgebraex1_44.gif)
](images/linearalgebraex1_45.gif)
](images/linearalgebraex1_46.gif)