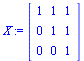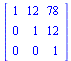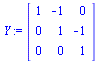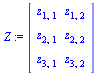>

restart;

 

>	with(LinearAlgebra);

 

>

 

Matrix operations 

Examples of matrix operations in Maple. First addition and scalar multiplication. If sizes do not match, then you get an error message. The data structure underlying matrices and vectors is called an rtable. Thus this word appears in error messages. 

>	A:=Matrix([[1,2,3],[3,2,1]]);

 

>	B:=Matrix([[-2,3,7],[7,5,9]]);

 

>

A+B;

 

>

2*B;

 

>

4*A-7*B;

 

>	C:=Matrix([[-1,2],[3,7]]);

 

>

A+C;

 

Error, (in rtable/Sum) invalid arguments

 

Matrix multiplication 

Here you have two possible forms of notation. First we use the shorthand notation, a period. 

>

C.A;

 

>	MatrixMatrixMultiply(C,A);

 

You will not need this longer form in the course, but it is important to use in cases where one needs to control memory usage, i.e. if the two matrices are very large. See the Maple documentation for details, if you need to use it. 

Powers of matrices are computed as follows. 

>	X:=Matrix([[1,1,1],[0,1,1],[0,0,1]]);

 

>

X^2;

 

>

X^3;

 

>

X^12;

 

You can compute the inverse of a matrix, using the power notation: 

>	Y:=X^(-1);

 

>

X.Y;

 

>

Y.X;

 

It is also possible to deal with matrices consisting of symbols. Here is an example of matrix multiplication for two matrices, a 2x2 and a 2x3 matrix. We redefine some of the variables used above. At the same time we show how to use an indexing function to name the entries. 

>	A:=Matrix(2,2,(i,j)->a[i,j]);

 

>	B:=Matrix(2,3,(i,j)->b[i,j]);

 

>

A.B;

 

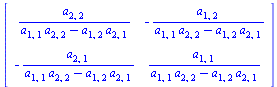
Check that the formula is the one you expect to get from the discussion in Lay. You can also get the formula for the inverse of a 2x2 matrix: 

>

A^(-1);

 

You can refer to the entries in a matrix using the Maple subscript notation: We give two examples, recalling the matrix first. 

>

B;

 

>

B[2,3];

 

>

C;

 

>

C[2,1];

 

An alternate way to get a matrix with symbol entries is the following: 

>	Z:=Matrix(3,2,symbol=z);

 

The transpose can be found in two different ways, as with all matrix operations. 

>	Transpose(Z);

 

>

Z^%T;

 

Warning: Note that now the indexing and the positions no longer agree. 

>