Opgave om Lagrangemetoden 1998


I uge 48 skal I bl.a. bruge tiden på at lave en stor opgave om Lagrangemetoden. Der er mulighed for at give opgaven forskellig sværhedsgrad, at nå langt eller knap så langt, og at vælge forskellig retning i den sidste del af opgaven.
Jeg regner med, at I laver den gruppevis eller evt. deler jer op i mindre grupper, hvis I finder det hensigtsmæssigt.
Opgaven afleveres senest 4/12 til mig enten direkte eller via intern post. Jeg vil ikke have Word eller Word Perfect filer på email, da det er besværligt for mig at få dem åbnet.

Her kommer så opgaven: Hovedideen er at gennemgå eksempler fra mikroøkonomi, hvor Lagrange og/eller Kuhn Tucker metoden kan bruges og eksempler, hvor den ikke kan bruges.

1.
Vælg et problem fra Mikroøkonomi, hvor man benytter optimering under bibetingelser. Eks: Maksimering af nytte under budgetrestriktion, minimering af omkostninger ved konstant output, maximering af output med konstante omkostninger, ...
2.
Behandl problemet så generelt som muligt, og som I synes I kan overskue: De ovennævnte eksempler er ikke enten eller. Der bør være diskussion af både generelle funktioner og konkrete eksempler, og jeg vil gerne se mindst tre variable behandlet. De sidste punkter kan I selv vælge generaliteten af.
3.
Giv gerne tegninger og løsninger via Maple.
4.
Hvilke egenskaber ved produktions-, profit-, omkostnings-, nytte, etc. funktioner gør, at S& H sætning 18.1 og 18.2 virker/ikke virker i de tilfælde, I har valgt?
5.
I kan få ideer til, hvornår metoden virker ved at se i Varian kapitel 3 med eksempler på preferencer. De kan overføres til eksempler på isokvanter (kapitel 17) og de andre eksempler ovenfor. Kan I se, hvad der går galt i de tilfælde, hvor Lagrange ikke giver max/min? Hvornår giver Lagrange flere kandidater?
6.
Kan I fortolke Lagrangemultiplikatoren (eller multiplikatorerne) 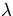$\lambda$ i jeres tilfælde?
Med venlig hilsen
Lisbeth Fajstrup

Lisbeth Fajstrup
11/19/1998