- Vægtet mindste kvadraters metode
- Den generelle fejlforplantningslov
- Repetition af diagonalisering, med introduktion til Cholesky dekomposition.
- Cederholm, afsnit 4.2
Opgaver
Opgave 1:
Der er givet fire punkter i planen: (0,0), (1, 0.9), (2, 1.1), (3, 1.5).
(a) Find den bedste rette linie ved hjælp af ikke-vægtet mindste kvadraters metode.
(b) De fire punkter tildeles vægtene hhv. 10, 1, 1, 1. Find den vægtede bedste rette linie.
(c) Tegn begge linier ind i et koordinatsystem. Beskriv hvilken effekt vægtene har på linien.
Opgave 2:
Der
er givet fire punkter D, E, F, G. Mellem hvert par af punkter har
vi målt en højdeforskel som angivet i nedenstående tabel. Desuden er
oplyst afstande mellem punkterne. (Disse antages at være eksakte.)
| Fra punkt | Til punkt | Højdeforskel | Afstand |
| D | E | 4 | 4 |
| F | D | 8 | 3 |
| F | E | 13 | 5 |
| F | G | 4 | 4 |
| G | D | 2 | 5 |
| G | E | 9 | 3 |
Det oplyses at E er et fikspunkt med højden 15.
(Opgave 2.1 og 2.2 benytter ikke oplysningerne om afstande.)
Opgave 2.1:
Opstil observationsligningen for de målte højdeforskelle. Opstil også normalligningen.
Opgave 2.2: (Denne delopgave udsættes til næste uge, idet der skal anvendes teori fra kursusgang 5 i opgaven.)
Lad A være designmatricen fra opgave 5.1 og lad y være observationsvektoren.
(a) Find Cholesky dekompositionen U af ATA.
(b) Find løsningen til normalligningen ved at løse først UTz=ATy, og dernæst Ux=z.
(c) Bestem Cholesky dekompositionen U2 af
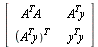 .
.
Hvad er sammenhængen mellem U og U2.
(d) Find kvadratsummen af residualerne φ ved hjælp af U2.
Opgave 2.3:
Variansen af målinger af højdeforskelle antages nu at være proportionale med de oplyste afstande.
(a) Bestem vægt-matricen C. Hvilke målinger får mest vægt og hvilke får mindst vægt.
(b) Find den vægtede mindste kvadraters løsning til ligningssytemet.
(c) Udregn variansfaktoren σ02.
(d) Bestem covariansmatricen.
Løsning til opgaver