Matematik 2 - Forår 2005

Reelle og Komplekse Funktioner

Thursday, April 14, 2005,  8:15
Room G5-112

Schedule

8:15-8:45

Review in G5-112.  We will review results on power series such as differentiability and radius of convergence, and give examples. We will also focus on the relationship between trigonometric functions and the exponential function.

8:45-10:45

Problem session. Work in groups.

10:45-12:00

Lecture in G5-112. We will define contour integrals and discuss some of their properties.

Problems

1. Prove Euler's formula:

exp(iz)=cos(z) + i sin(z), for all z∈C.

 

2. (a) Show that exp(z) has no zeros in C.

    (b) Find the solutions to the equation: exp(z)=1.

 

3. Find the radius of convergence for the series .

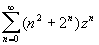4.Suppose we know that the series 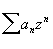converges at z=1-i and diverges at z=5. What can you say about its radius of convergence? (i.e., find inequalities of the type r≤a, b≤r).

5. Find the zeros of the function sin(z).