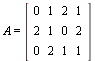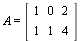Lineær algebra - 2

Onsdag den 11. september 2013, 10.15-12.00

Emne:

• Ortogonal projektion,  afsnit 6.3 i SIF
  
• Mindste kvadraters metode,  afsnit 6.4 i SIF
  
• Anvendelse i landmåling
  

Slides

Opgaveregning:

Opgaver 

1. SIF, opgave 6.4.5
   
    
2. SIF, opgave 6.3.21
   
   
3. Bestem en basis for hver af de fire fundamentale underrum (Col A, Row A = Col A^T, Nul A, Nul A^T) for matricen
   
   
   
    
4. SIF, opgave 6.3.1
    
5. Betragt matricen
   
   
   
   (a)  Find en basis for nulrummet for A, og vis at den er ortogonal på rækkerummet for A.
   (b)  Lad x = (3,3,3). Skriv x som sum af en vektor i nulrummet for A og en vektor i rækkerummet for A.
    
6. Diskuter i gruppen mindste kvadraters metode - hvad er det grundliggende princip og hvorfor giver det mening at følge dette princip.
    
   
7. Mellem de fire punkter A, B, C og D er der målt højdeforskelle som angivet i tabellen:
   

   Fra punkt	Til punkt	Højdeforskel
   C	A	10
   A	B	5
   C	B	14
   C	D	4
   D	A	2
   D	B	9

   (a)  Opstil observationsligningen (Cederholm, afsnit 2.2) for dette system.
   (b)  Det oplyses nu at C er et fikspunkt med højden 1. Opstil observationsligningen for dette nye system.
   (c)  Hvad er forskellen mellem ligningerne i (a) og (b) ?
   (d)  Find mindste kvadraters løsning til observationsligningen ved at finde og løse normalligningen.

Facit