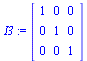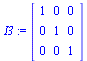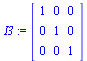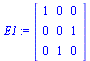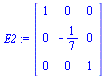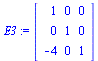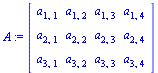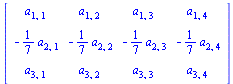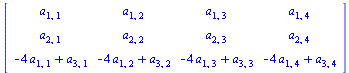>

restart;

 

>	with(LinearAlgebra):

 

Matrix operations 2 

Some further examples of matrix operations. The first thing to note is that for example the identity matrix generated in Maple cannot be modified. This is shown here. Note also that some symbols are reserved, so you cannot name an identity matrix as `I` 

>	I:=IdentityMatrix(3);

 

Error, illegal use of an object as a name

 

>	I3:=IdentityMatrix(3);

 

>	I3[3,1]:=-4;

 

Error, invalid assignment of non-zero to identity off-diagonal

 

So if we need to generate an identity matrix we can modify we need to do it ourselves. Here is a very general approach that uses an indexing function (procedure) to generate the identity matrix. It works irrespective of the size of the matrix, since the matricx size is obtained from the Matrix constructor. First the function: 

>	f:=(i,j)->if i=j then 1 else 0 end if;

 

>	I3:=Matrix(3,3,f);

 

Elementary matrices 

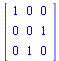
We now modify this identity matrix to give examples of the elementary matrices. The first one is the interchange of row 2 and row 3. We will generate it using the general row operations command. 

>	E1:=RowOperation(I3,[2,3]);

 

The second elementary matrix is one that multiplies row 2 by -1/7. 

>	E2:=RowOperation(I3,2,-1/7);

 

The third elementary matrix multiplies row 1 by -4 and adds to row 3 

>	E3:=RowOperation(I3,[3,1],-4);

 

Now we illustrate the fact that multiplication by the left with an elementary matrix carries out the corresponding row operation. We take a general 3x4 matrix and do the three computations. 

>	A:=Matrix(3,4,symbol=a);

 

>

E1.A;

 

>

E2.A;

 

>

E3.A;

 

We also illustrate the fact that the inverse of an elementary matrix will undo the original row operation. Here are the three inverse matrices. 

>

E1^(-1);

 

>

E2^(-1);

 

>

E3^(-1);

 

>