Lineær Algebra - 22. kursusgang, mandag den 9. december

Mere om ortogonale matricer.
Desuden Afsnit 6.5, side 419-421: Flytninger.
Noget om hvordan eksamen foregår, se www.tnb.aau.dk/index.php?id=15307  og  www.first.math.aau.dk/linear-algebra-da/

Slides
Tavle

Opgaveregning 13.15-16.15

Opgaver i afsnit 6.5:

• Er den givne matrix ortogonal.
  Opgaver: 1, 4, 5, 3
• Afgør om en ortogonal 2x2 matrix er standardmatrix for en rotation eller en spejling. Find spejlingsakse eller rotationsvinkel.
  Opgaver: 9, 11
• Ortogonale matricer og egenværdier.
  Opgave: 49
• Flytninger i planen. Bestem Q og b så F(v)=Qv+b.
  Opgaver: 61, 63
• Rotationer i rummet.
  Lad Q_x og Q_z  være matricerne for rotation på 90^o om henholdsvis x-aksen og z-aksen:
  
  
  
  Lad Q=Q_xQ_z være matricen for rotation 90^o om z-aksen efterfulgt af rotation 90^o om x-aksen.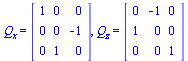
  Q er også en rotation. Bestem egenrummet hørende til egenværdien 1 og dermed rotationsaksen for Q .  Facit
  

Eksamensopgaverne fra Ordinær eksamen 2012: 
http://www.first.math.aau.dk/linear-algebra-da/tidligere-eksamensopgaver/


Ingen forelæsning efter opgaveregningen.