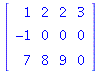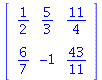syntax.mw
Maple syntax og MapleTA
Nedenfor er en kort gennemgang af nogle aspekter af Maple syntax, som er vigtige i forbindelse med indtastning af svar i MapleTA.
Operatorernes rækkefølge
Vi har følgende operationer med tal (og symboler), som udføres i denne rækkefølge:
1. potensopløftning, angivet med operatoren ^ Et par eksempler er
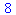 |
(1) |
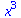 |
(2) |
2. multiplikation og division. Operatorerne er * og / Bemærk at disse to operationer kommuterer, dvs rækkefølgen er uden betydning. Et par eksempler
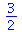 |
(3) |
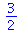 |
(4) |
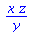 |
(5) |
3. addition og subtraktion. Operatorerne er + og - Igen kommuterer de to operationer, så at rækkefølgen er uden betydning. Et par eksempler
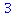 |
(6) |
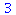 |
(7) |
Rækkefølgen bliver af betydning, når man blander de tre klasser af operationer. Reglen er at først udføres potensopløftning, dernæst multiplikation og division, og til sidst addition og subtraktion. Et par eksempler.
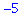 |
(8) |
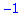 |
(9) |
Parenteser
Parenteser bruges på mange forskellige måder i Maple og dermed også i MapleTA. Det er vigtigt at skelne mellem de tre forskellige typer af parenteser: De almindelige runde parenteser, som ( ). De bruges som man er vant til. For eksempel til at bestemme rækkefølgen af operationer, som i eksemplet
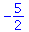 |
(10) |
Lister
Lister er en datatype der bruges meget i Maple og MapleTA. Den angives ved hjælp af firkantede parenteser, som [ ] Her er et par eksempler. Bemærk, at indgangene i en liste har en bestemt position. To tal i forskellig rækkefølge giver to forskellige lister.
Man kan afgøre, om to objekter eller udtryk er ens i mange tilfælde (men ikke i alle), ved at bruge funktionen
evalb Hvis de to udtryk er ens, er svaret true, og ellers false.
![[1, 2]](images/syntax_11.gif)
![[2, 1]](images/syntax_12.gif) |
(11) |
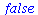 |
(12) |
![[1, 2, 2]](images/syntax_14.gif) |
(13) |
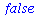 |
(14) |
Mængder
Der er forskel mellem mængder og lister. I en mængde betyder rækkefølge ikke noget, og gentagelser heller ikke noget. Mængder angives med { } . Vi gentager eksemplerne ovenfor med mængder i stedet for lister.

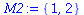 |
(15) |
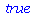 |
(16) |
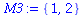 |
(17) |
Vigtigt!
Man kan ikke udelade komma i mængde og liste. Bemærk forskellen til syntax i matlab. Hvis man udelader det, får man en fejl.
Vektorer
Der er mange forskellige måder at angive en vektor på i Maple, og dermed som input til MapleTA. Vi får primært brug for at kunne angive søjlevektorer. Vi vælger en måde at gøre det på, som nok volder de færreste problemer. Her er nogle eksempler.
](images/syntax_20.gif) |
(18) |
](images/syntax_21.gif) |
(19) |
Når indgangene er tal, kan man skrive algebraiske operationer ind som en del af indgange. De bliver automatisk regnet ud, før matricen vises.
| > |
Vector([1-2,1/3+1,1/2-1/3]); |
](images/syntax_22.gif) |
(20) |
Man kan få en rækkevektor på følgende måde.
| > |
Vector[row]([1,2,3,4]); |
](images/syntax_23.gif) |
(21) |
Matricer
Matricer kan defineres på mange måder. Vi viser her hvordan det kan gøres ved hjælp af en liste af lister. Her er nogle eksempler.
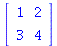 |
(22) |
| > |
Matrix([[1,2,2,3],[-1,0,0,0],[7,8,9,0]]); |
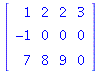 |
(23) |
Man kan give algebraiske udtryk med tal, som bliver udregnet før matricen vises.
| > |
Matrix([[1-1/2,2-1/3,3-1/4],[3/7*2,2-3,4-1/11]]); |
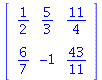 |
(24) |
Advarsel
Der findes en kortfattet måde at skrive små vektorer og matricer på. Den må man ikke anvende i MapleTA. Det fører til at svaret bliver bedømt som forkert, selv om det var den rigtige vektor. For eksempel må man ikke bruge
](images/syntax_27.gif) |
(25) |
![]()
![]()