In modern computers (or computer networks), calculations are typically
no longer perfomed sequentially (``one step at a time'') but in
cooperation between several processors doing parts of the job ``in
parallel''. Through concurrency, one aims to save time and memory. To
do so, the proper scheduling of processors is a crucial task. Some of
the issues involved are to make sure that the calculation does not
stop (no deadlocks), and that the result is correct for all
possible schedules. In many instances, it seems to be difficult to
prove the correctness of a concurrent program under all possible
circumstances, and this is certainly one of the reasons why
concurrency is not applied as much as one would hope for, in
particular in critical software.
One of the difficulties is to obtain feasible mathematical models for
concurrent computations. Moderate success has been achieved by applying
transition models of a graph-theoretic nature, like one does for modelling
sequential computation. However this approach seems to have a fundamental
restriction to its applicability by the so-called ``state space explosion
problem:'' In most models, the number of states grows exponentially in the
number of processors, and it will therefore often be impossible to handle
the complexity of the state space.
It has hence been important to be able to reduce the number of
states by handling states with the same ``potential'' as being
equivalent. How can one formulate this potential in mathematical terms?
Here it seems, that ideas and methods from the geometric/topological
world can play a role. A small but growing group of researchers on the
interface between topology and theoretical computer science has been
working on concurrency models that allow one to formulate interesting
notions with the potential to facilitate the future development of
algorithms.
To say it briefly, one replaces a (huge) discrete state space by a
continuous model, whose main additional feature is the existence of
directed paths (dipaths) corresponding to transitions in the
original model. It is important that executions (transitions), that
are equivalent for structural reasons - not only by chance - can be
deformed into each other by a geometric process (oriented homotopy or
dihomotopy).
Figure 1:
A simple 2-dimensional state space with oriented paths
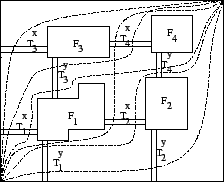 |
This observation makes it plausible and interesting to try to apply
ideas and methods from the mathematical discipline algebraic
topology, which has the study of maps up to deformations as its
subject. In algebraic topology, one tries to develop algebraic (often
discrete) images of continuous geometric properties, which are robust
under deformations and to filter out essential information in these
invariants. The overall idea is thus to define and investigate
discrete invariants of the continuous state space, that can reveal
essential properties of both that space and of the discrete state
space that was the starting point.
It turns out, that one cannot directly apply the traditional algebraic
topological machinery. The computer scientific applications demand
preferred directions which destroy an overall symmetry that is usually
assumed. This change in assumptions needs to be taken care of. For
example, the first and most important invariant of a space, its
fundamental group, has to be replaced by the fundamental
category of a space with preferred directions (po-space,
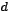 -space, flow etc. in the terminology developed so-far). Thus, the
newly emerging discipline investigating state spaces by geometric
means places itself on the cross-roads between computer science,
topology, geometry (amongst others some features of relativity theory)
and, increasingly, category theory. Another computer science subject
borrowing methodology from Algebraic Topology is the area of
Distributed Computing (Herlihy, Rajsbaum [11] et al.)
-space, flow etc. in the terminology developed so-far). Thus, the
newly emerging discipline investigating state spaces by geometric
means places itself on the cross-roads between computer science,
topology, geometry (amongst others some features of relativity theory)
and, increasingly, category theory. Another computer science subject
borrowing methodology from Algebraic Topology is the area of
Distributed Computing (Herlihy, Rajsbaum [11] et al.)
Lisbeth Fajstrup and Martin Raussen were first thrilled by some germs
of the field described above when participating in the conference
New Connections between Mathematics and Computer Science at the
Isaac Newton Institute, Cambridge, UK, in November 1995. We started to
work on a limited aspect of this field, the automatic recognition of
deadlocks and unsafe regions using a geometric idea. This idea was
developed [3], both theoretically and in an algorithm, in
collaboration with Dr. Éric Goubault, now a senior researcher at
Commissariat à l'énergie atomique, Saclay, France.
Dr. Goubault is a computer scientist combining a very broad
mathematical literacy with an eye for algorithms and applications.
This collaboration has extended since. In recent years, we have mainly
been working on a better understanding of the fundamental category of
models for state spaces. In particular, we want to arrive at
``compressed'' categories with the same (or most of the same)
information. This has certainly an aspect of fundamental research.
Classical algebraic topological methodology has to be extended by, for
example, applying category theoretical tools. Several attempts have
already been published [8,14,2], but there are lots
of open ends. To mention a few: the development of homology categories
(in the same spirit as the fundamental category, with nicer algebraic
properties and with calculational tools), the application of naturality
properties, and a better understanding of homotopy invariance and its
limits etc.
consists right now of
- Lisbeth Fajstrup, associate professor, Dept. Math. Sci.
- Martin Raussen, associate professor, Dept. Math. Sci.
- Rafael Wisniewski, associate professor, Dept. Control Theory,
currently working on his 2nd Ph.D. in this area (advisor: Martin
Raussen; 1st Ph.D. in control engineering)
- Ulrich Fahrenberg, Ph.D.-student (advisors: Lisbeth Fajstrup and
Martin Raussen)
We also have a collaboration with researchers in theoretical computer
science at Aalborg University, notably Prof. Kim G. Larsen,
Prof. A. Ravn, assoc. professors L. Aceto and A. Ingolfsdottir. We
have occasionally held joint seminars.
One of the challenges in view of algorithmic applications, is to
understand and to exploit compositionality. That is, to be able
to calculate invariants of the total space from invariants of
(well-chosen) pieces together with information about the interplay
between these local invariants. The essential tool, a Seifert-van
Kampen theorem for fundamental categories (and similar gadgets) has
recently been proved[9] by the Italian topologist and
category theorist Marco Grandis at Genova. It is a major challenge to
combine this result with our ``compression approach'' to categories. A
good understanding should be rewarded with a lucid algorithm
describing the borders of regions of states with ``equivalent
potential'' in state spaces. This would generalise an algorithmic idea
already presented in [13].
Several researchers, in particular Philippe Gaucher at Paris Jussieu,
have argued for the application of model category tools
into the subject. This abstract approach - going back to Quillen's
axiomatic homotopy theory from around 1970 - seems to supply important
notions and a more abstract point of view, that has the potential of
admitting comparisons between various models (abstract notions of
equivalences, fibrations, cofibrations etc.)
Cooperation has been vital for the development of this subject. We
started a series of workshops (GETCO): The first was held in Aalborg
in 1999, followed up by Penn State (2000), Aalborg (2001), Toulouse
(2002), Marseille (2003). Another important gathering was the
conference Algebraic Topological Methods in Computer Science
organised by G. Carlsson and R. Jardine at Stanford University, USA.
The proceedings of that conference have appeared as the special volume
5, no.2, of Homology, Homotopy Appl. We have several
times in recent years organised small international workshops about
these topics at Aalborg University. Over time, these efforts have
resulted in the following list of our most important international
collaborators (cf. also the GETCO
webpage).
- Prof. R. Brown, Bangor University, UK
- Dr. P. Gaucher, IRMA, Univ. Paris 7, France
- Dr. É. Goubault, CEA, Gif-sur-Yvette, France
- Prof. Marco Grandis, Univ. Genova. Italy
- Dr. J. Gunawardena, Harvard University, Boston, USA
- Mr. E. Haucourt, CEA, Gif-sur-Yvette, France
- Prof. M. Herlihy, Brown University, Providence, RI, USA
- Prof. Kathryn Hess, EPFL Lausanne, Switzerland
- Prof. T. Porter, Bangor University, UK
- Prof. V. Pratt, Stanford University, USA
- Dr. S. Rajsbaum, UNAM, Mexico
- Dr. S.Sokolowski, Polish Academy of Sciences, Gdansk, Poland
Almost all of our collaborators have visited Aalborg for shorter or longer
periods. Lisbeth Fajstrup and Martin Raussen have had extended stays
for collaboration in Paris; in 2002, for a month as invited guest
researchers at École Polytechnique, Paris, France. Martin Raussen
visited Brown University, Providence, RI, and Compaq Research
Laboratories, Boston, MA, USA, in the year 2000. He has been a
coorganisor of a ``summer school'' on our subject with the conference
LATIN 2002 - Latin American Theoretical Informatics, Cancun, Mexico.
- 1
-
L. Fajstrup.
Dicovering spaces.
Homology, Homotopy, Appl., 5(2):1-17, 2003.
- 2
-
L. Fajstrup, É. Goubault, E. Haucourt, and M. Raussen.
Components of the fundamental category.
Technical Report R-2003-02, Department of Mathematical Sciences.
Aalborg University, 2003.
to appear in Appl. Categ. Structures.
- 3
-
L. Fajstrup, É. Goubault, and M. Raussen.
Detecting Deadlocks in Concurrent Systems.
In D. Sangiorgi and R. de Simone, editors, CONCUR '98;
Concurrency Theory, volume 1466 of Lect. Notes Comp. Science, pages
332 - 347, Nice, France, September 1998. Springer-Verlag.
9th Int. Conf., Proceedings.
- 4
-
L. Fajstrup, É. Goubault, and M. Raussen.
Algebraic topology and concurrency.
Technical Report R-99-2008, Department of Mathematical Sciences,
Aalborg University, DK-9220 Aalborg Øst, June 1999.
conditionally accepted for publication in Theoret. Comput. Sci.
- 5
-
P. Gaucher and É. Goubault.
Topological Deformation of Higher Dimensional Automata.
Homology, Homotopy, Appl., 5(2):39-82, 2003.
- 6
-
É. Goubault.
Geometry and concurrency: A user's guide.
Math. Structures Comput. Sci., 10(4):411-425, 2000.
- 7
-
É. Goubault.
Some Geometric Perspectives in Concurrency Theory.
Homology, Homotopy, Appl., 5(2):95-136, 2003.
- 8
-
É. Goubault and M. Raussen.
Dihomotopy as a tool in state space analysis.
In S. Rajsbaum, editor, LATIN 2002: Theoretical Informatics,
volume 2286 of Lect. Notes Comput. Sci., pages 16 - 37, Cancun,
Mexico, April 2002. Springer-Verlag.
- 9
-
M. Grandis.
Directed Homotopy Theory I. The Fundamental Category.
Technical Report 443, Dip. di Matematica dell' Univ. di Genova, 2001.
to appear in Cahiers Top. Géom. Diff. Catég.
- 10
-
J. Gunawardena.
Homotopy and concurrency.
Bulletin of the EATCS, 54:184-193, 1994.
- 11
-
M. Herlihy and S. Rajsbaum.
A Primer on Algebraic Topology and Distributed Computing.
volume 1000 of Lecture Notes in Comput. Sci., pages 203-217.
Springer-Verlag, 1995.
- 12
-
V. Pratt.
Modelling concurrency with geometry.
Proc. of the 18th ACM Symposium on Principles of Programming
Languages., pages 311-322, 1991.
- 13
-
M. Raussen.
On the classification of dipaths in geometric models for concurrency.
Math. Structures Comput. Sci., 10(4):427-457, 2000.
- 14
-
M. Raussen.
State spaces and dipaths up to dihomotopy.
Homology, Homotopy Appl., 5(2):257-280, 2003.
Martin Raussen
2003-12-17

![]() -space, flow etc. in the terminology developed so-far). Thus, the
newly emerging discipline investigating state spaces by geometric
means places itself on the cross-roads between computer science,
topology, geometry (amongst others some features of relativity theory)
and, increasingly, category theory. Another computer science subject
borrowing methodology from Algebraic Topology is the area of
Distributed Computing (Herlihy, Rajsbaum [11] et al.)
-space, flow etc. in the terminology developed so-far). Thus, the
newly emerging discipline investigating state spaces by geometric
means places itself on the cross-roads between computer science,
topology, geometry (amongst others some features of relativity theory)
and, increasingly, category theory. Another computer science subject
borrowing methodology from Algebraic Topology is the area of
Distributed Computing (Herlihy, Rajsbaum [11] et al.)